Tabla de contenidos    Indice temático   

Detalles complementarios

Los coeficientes a, b, c y d de la ecuación proporcionan información detallada de los elementos más importantes de la hipérbola.

$\begin{array}{l} y=\frac{ax+b}{cx+d}\\ \text{Tomando }x=\mathrm{0\; }\text{se obtiene }y=b/d\text{ que es la ordenada}\\ \text{en el origen}\text{, punto de corte de la curva con el eje }Y\text{.}\\ \text{Tomando }y=\mathrm{0\; }\text{se obtiene }ax+b=0\text{ y }x=-b/a\text{ que}\\ \text{es el punto de corte de la curva con el eje }X\text{.}\\ \text{El denominador se anula en }x=-d/c\text{ , que resulta ser}\text{,}\\ \text{por tanto}\text{, la ecuación de la asíntota vertical}\text{.}\end{array}$

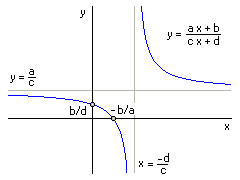La ecuación de la asíntota horizontal se obtiene tras efectuar la división euclídea:

Con lo que se obtiene:

$y=\frac{ax+b}{cx+d}=\frac{a}{c}+\frac{b-ad/c}{cx+d}=\frac{a}{c}+\frac{\left(bc-ad\right)/c^2}{x+d/c}=\frac{a}{c}+\frac{k}{x+d/c}$

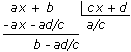
Que resulta ser la función de proporcionalidad inversa  y = k/x  [con k = (bc −ad)/c²]  desplazada horizontalmente d/c unidades y verticalmente a/c unidades, por lo que y = a/c es la ecuación de la asíntota horizontal.

No se preocupe si le parece complicado, pues un estudio más detallado de las "ramas infinitas" (como es el caso de estas ramas asíntóticas) se aborda al final de esta unidad.