Curvas que no son funciones
Ya se ha visto cómo las funciones pueden ser representadas gráficamente, dando origen a distintas curvas. De forma recíproca, las herramientas que proporciona el Análisis (rama de las Matemáticas en la que se estudian las funciones) pueden ser empleadas en Geometría para el estudio de las curvas.
Condición indispensable para que una función esté bien determinada es que a cada valor x perteneciente al dominio le corresponda un único valor y del recorrido. ¿Qué hacer con una curva en la que a cada valor de x le correspondan dos de y? ¿Serán inservibles las herramientas del Análisis?
¿Qué hacer con la parábola x − y2 −1 = 0 ( )?
|
El problema: curva que NO es función 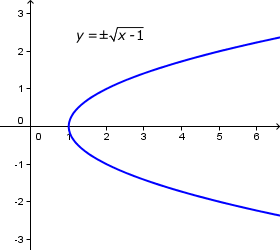
|
La solución: una curva y dos funciones 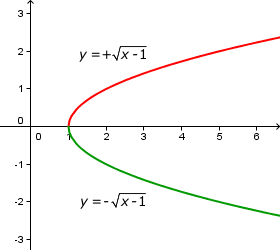
|
La solución ha resultado sencilla, no hay más que descomponer la curva en dos trozos, correspondiendo cada uno de ellos a una función distinta. A partir de aquí se pueden estudiar como funciones cada una de las dos ramas de la parábola.