notas02e

Rectas paralelas

Si se tienen las rectas

r₁: y = 2x + 3

r₂: y = mx - 1

¿cuál ha de ser el valor de m para que las rectas sean paralelas?

Obviamente, m = 2; pues solo dos rectas que tengan la misma pendiente serán paralelas.

En general, dadas dos rectas en forma explícita:

r₁: y = m₁x + n₁

r₂: y = m₂x + n₂

si m₁ = m₂ y n₁ ≠ n₂ las rectas son PARALELAS.

(Si m₁ = m₂ y n₁ = n₂, las rectas son coincidentes, son la misma recta).

¿Y si las rectas están en forma general (implícita)?

r₁: A₁x + B₁y + C₁ = 0

r₂: A₂x + B₂y + C₂ = 0

Sus vectores normales ${\vec{n}}_{1} = (A_{1}, B_{1}) y {\vec{n}}_{2} = (A_{2}, B_{2})$ también serán paralelos y, por tanto, combinación lineal el uno del otro, proporcionales:

r₁: A₁x + B₁y + C₁ = 0

r₂: A₂x + B₂y + C₂ = 0

si $\frac{A_{1}}{A_{2}} = \frac{B_{1}}{B_{2}} \neq \frac{C_{1}}{C_{2}}$ las rectas son PARALELAS.

(Si $\frac{A_{1}}{A_{2}} = \frac{B_{1}}{B_{2}} = \frac{C_{1}}{C_{2}}$ , las rectas son coincidentes, son la misma recta).

Si las rectas vienen dadas en forma paramétrica

$r : {\begin{array}{l} x = a_{1} + t u_{1} \\ y = a_{2} + t u_{2} \end{array} s : {\begin{array}{l} x = b_{1} + t v_{1} \\ y = b_{2} + t v_{2} \end{array}$

Serán paralelas cuando lo sean sus vectores de dirección $\vec{u} (u_{1}, u_{2}) y \vec{v} (v_{1}, v_{2})$ , lo que ocurrirá cuando sus coordenadas sean proporcionales:

$r : {\begin{array}{l} x = a_{1} + t u_{1} \\ y = a_{2} + t u_{2} \end{array} s : {\begin{array}{l} x = b_{1} + t v_{1} \\ y = b_{2} + t v_{2} \end{array}$

si $\frac{u_{1}}{v_{1}} = \frac{u_{2}}{v_{2}}$ y, además, el punto A (a₁, a₂) no pertenece a la recta s, o el punto B (b₁, b₂) no pertenece a r, las rectas son PARALELAS.

(Si, siendo proporcionales los dos vectores, el punto A (a₁, a₂) pertenece a la recta s, o el punto B (b₁, b₂) pertenece a r, las rectas son coincidentes).

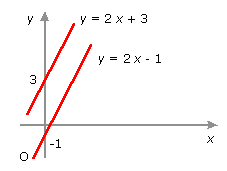
rectas paralelas con m = 2

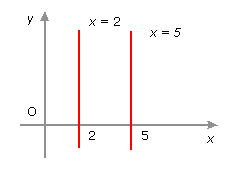
rectas paralelas al eje OY

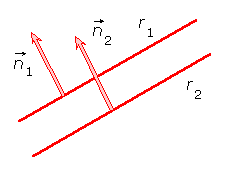
rectas paralelas (con vectores normales)

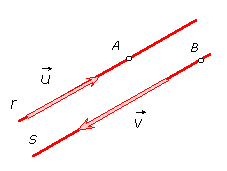
rectas paralelas (con vectores de dirección)