Se llama así, ecuación reducida, a la que se obtiene tomando como origen de coordenadas el centro de la hipérbola y como ejes coordenados los ejes de simetría de la hipérbola.

| d (P, F) - d (P, F') |= k = 2a

sustituyendo en las fórmulas que calculan la distancia entre dos puntos:

$\left|\sqrt{{\left(x-c\right)}^2+y^2}-\sqrt{{\left(x+c\right)}^2+y^2}\right|=2a$

al quitar las barras de valor absoluto resulta:

$\sqrt{{\left(x-c\right)}^2+y^2}-\sqrt{{\left(x+c\right)}^2+y^2}=\pm 2a$

procediendo de forma análoga a como se hizo con la elipse, se llega a la expresión:

$\left(c^2-a^2\right)x^2-a^2{y}^2=a^2\left(c^2-a^2\right)$

sustituyendo $c^2-a^2=b^2$

$b^2{x}^2-a^2{y}^2=a^2{b}^2$

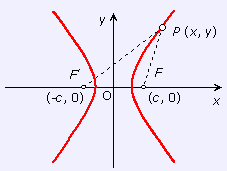dividiendo, por último, los dos miembros por $a^2{b}^2$, resulta: