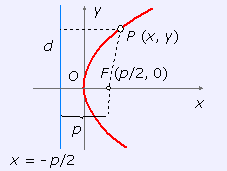Se llama así, ecuación reducida, a la que se obtiene tomando como origen de coordenadas el vértice de la parábola y como eje de abscisas el eje de simetría de la parábola. El foco aparece así situado en (p/2, 0) y la ecuación de la directriz resulta ser x = - p/2 .

d (P, F) = d (P, d)

sustituyendo en las fórmulas que calculan la distancia entre dos puntos y la distancia de un punto a una recta:

$\sqrt{{\left(x-\frac{p}{2}\right)}^2+y^2}=x+\frac{p}{2}$

elevando al cuadrado ambos miembros y simplificando: